Pullback (category theory)
In category theory, a branch of mathematics, a pullback (also called a fiber product, fibre product, fibered product or Cartesian square) is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain; it is the limit of the cospan 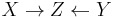 . The pullback is often written
. The pullback is often written
Contents |
Universal property
Explicitly, the pullback of the morphisms f and g consists of an object P and two morphisms p1 : P → X and p2 : P → Y for which the diagram
commutes. Moreover, the pullback (P, p1, p2) must be universal with respect to this diagram. That is, for any other such triple (Q, q1, q2) for which the following diagram commutes, there must exist a unique u : Q → P (called mediating morphism) such that 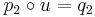 and
and 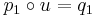
As with all universal constructions, the pullback, if it exists, is unique up to a unique isomorphism.
Weak pullbacks
A weak pullback of a cospan X → Z ← Y is a cone over the cospan that is only weakly universal, that is, the mediating morphism u : Q → P above need not be unique.
Examples
In the category of sets, a pullback of f and g is given by the set
together with the restrictions of the projection maps 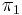 and
and 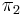 to X × Z Y .
to X × Z Y .
Alternatively one may view the pullback in Set asymmetrically:
where 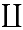 is the disjoint (tagged) union of sets (the involved sets are not disjoint on their own unless f resp. g is injective). In the first case, the projection
is the disjoint (tagged) union of sets (the involved sets are not disjoint on their own unless f resp. g is injective). In the first case, the projection 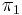 extracts the x index while
extracts the x index while 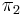 forgets the index, leaving elements of Y.
forgets the index, leaving elements of Y.
- This example motivates another way of characterizing the pullback: as the equalizer of the morphisms f o p1, g o p2 : X × Y → Z where X × Y is the binary product of X and Y and p1 and p2 are the natural projections. This shows that pullbacks exist in any category with binary products and equalizers. In fact, by the existence theorem for limits, all finite limits exist in a category with a terminal object, binary products and equalizers.
Another example of a pullback comes from the theory of fiber bundles: given a bundle map π : E → B and a continuous map f : X → B, the pullback X ×B E is a fiber bundle over X called the pullback bundle. The associated commutative diagram is a morphism of fiber bundles.
In any category with a terminal object Z, the pullback X ×Z Y is just the ordinary product X × Y.[1]
Preimages
Preimages of sets under functions can be described as pullbacks as follows: Suppose
- f : A → B
and
- B0 ⊆ B.
Let g be the inclusion map B0 ↪ B.
Then a pullback of f and g (in Set) is given by the preimage f-1 [ B0 ] together with the inclusion of the preimage in A
- f-1 [ B0 ] ↪ A
and the restriction of f to f-1 [ B0 ]
- f-1 [ B0 ] → B0.
Properties
- Whenever X ×ZY exists, then so does Y ×Z X and there is an isomorphism X ×Z Y
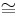 Y ×ZX.
Y ×ZX. - Monomorphisms are stable under pullback: if the arrow f above is monic, then so is the arrow p2. For example, in the category of sets, if X is a subset of Z, then, for any g : Y → Z, the pullback X ×Z Y is the inverse image of X under g.
- Isomorphisms are also stable, and hence, for example, X ×X Y
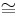 Y for any map Y → X.
Y for any map Y → X. - Any category with pullbacks and products has equalizers.
See also
- The categorical dual of a pullback is a called a pushout.
- Product (Category Theory)
- Pullbacks in differential geometry
- Equijoin in relational algebra.
Notes
- ^ Adámek, p. 197.
References
- Adámek, Jiří, Herrlich, Horst, & Strecker, George E.; (1990). Abstract and Concrete Categories (4.2MB PDF). Originally publ. John Wiley & Sons. ISBN 0-471-60922-6. (now free on-line edition).
- Cohn, Paul M.; Universal Algebra (1981), D.Reidel Publishing, Holland, ISBN 90-277-1213-1 (Originally published in 1965, by Harper & Row).
External links
- Interactive Web page which generates examples of pullbacks in the category of finite sets. Written by Jocelyn Paine.
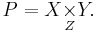
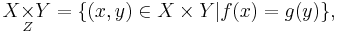
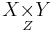
![\cong
\coprod_{x\in X} g^{-1}[\{f(x)\}]](/2012-wikipedia_en_all_nopic_01_2012/I/910c955a09608315aeeb2f4a09fb6ebf.png)
![\cong
\coprod_{y\in Y} f^{-1}[\{g(y)\}]](/2012-wikipedia_en_all_nopic_01_2012/I/e04821da2d6821099d751bcb4f88c60c.png)